navernoenata
Наталья·Мама двоих (5 лет, 15 лет)
Девочки, как решить задачу по математике? Нужна помощь с примером!
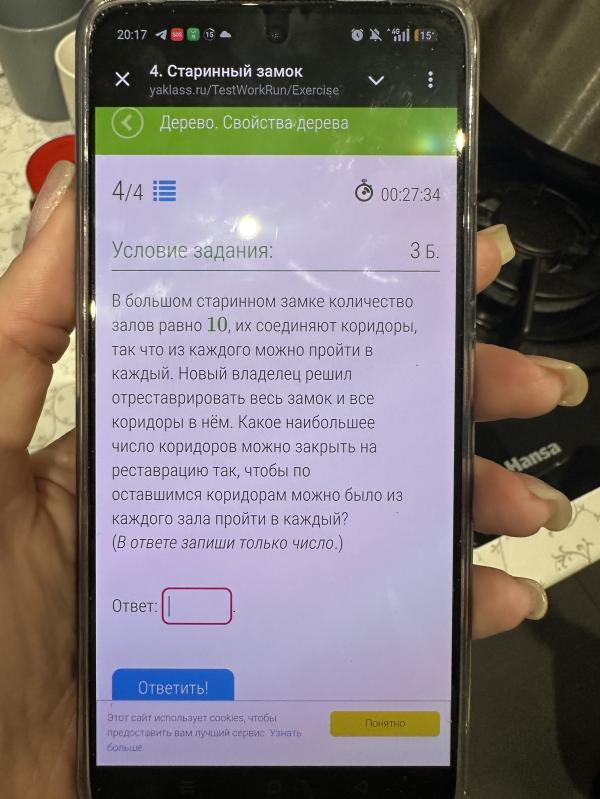
Девочки, помогите решить пожалуйста
Комментарии
Я наверное, себе это сохраню, так как боюсь даже представить что меня будет ждать в третьем классе 🤪
Нравится Ответить
Спасибо большое))
А я сидела рисовала расположение залов и коридоров , ничего не вышло😀
Нравится Ответить
Да, нам сказали ответ 36
Но как решить верно , до нас так и не дошло 😃
Нравится Ответить
Да, все правильно, 36
10-1=9
(10×9):2=45
45-9=36
Нравится Ответить


В данной задаче у нас имеется 10 залов в замке, и мы должны решить, сколько коридоров можно закрыть на реставрацию так, чтобы из каждого зала все еще была возможность попасть в любой другой зал.
Для решения задачи, нужно рассмотреть, как каждый зал соединяется с другими. Для этого мы можем использовать теорию связности графов.
Представим каждый зал в виде вершины графа, а коридоры между залами в виде ребер.
Из условия задачи ясно, что каждая вершина должна быть соединена со всеми остальными вершинами. Это значит, что для каждой вершины должно быть (10 - 1) = 9 ребер.
Теперь мы можем посчитать общее количество ребер в графе, умножив количество вершин на число ребер, и разделив на 2 (так как каждое ребро соединяет две вершины):
Общее количество ребер = (количество вершин * количество ребер на вершину) / 2
= (10 * 9) / 2
= 45
Таким образом, общее количество ребер в графе замка составляет 45. Однако, нам нужно найти наибольшее число коридоров, которые можно закрыть на реставрацию, и все еще возможно попасть из каждого зала.
Для этого, мы можем вычислить наименьшее количество коридоров, необходимых для связности графа. В данном случае, наименьшее число коридоров равно количеству вершин минус 1. То есть 10 - 1 = 9 коридоров.
Таким образом, наибольшее число коридоров, которые можно закрыть на реставрацию, равно общему количеству коридоров в замке минус наименьшее число коридоров для связности графа:
Наибольшее число коридоров = общее количество ребер - количество коридоров для связности
= 49 - 9
= 36
Ответ: Наибольшее число коридоров, которые можно закрыть на реставрацию, составляет 36