Как решить задачу?

Девочки спасибо вам огромное!!! Вы помогли сделать дз🌸🌸🌸

Если НОА И СОВ равны, то равны и их элементы ОА=ОВ, СВ=АН, НАО=СВО, СЛЕДОВАТЕЛЬНО треугольник АОВ равнобедренный и углы ОАВ=ОВА
углы А и В равны, потому что состоят из двух равных углов.
Треугольники САВ и НАВ равны по 1 признаку равенства треугольников, АВ общая

Девочки спасибо вам огромное!!! Вы помогли сделать дз🌸🌸🌸

Я только вспомнила теорему Пифагора, может её сюда приплести

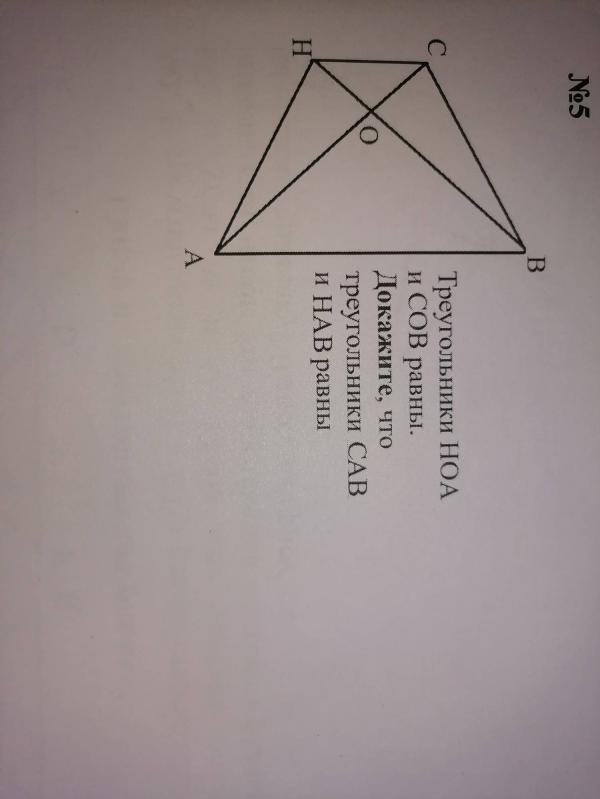
Если НОА И СОВ равны, то равны и их элементы ОА=ОВ, СВ=АН, НАО=СВО, СЛЕДОВАТЕЛЬНО треугольник АОВ равнобедренный и углы ОАВ=ОВА
углы А и В равны, потому что состоят из двух равных углов.
Треугольники САВ и НАВ равны по 1 признаку равенства треугольников, АВ общая

Тк треугольники Ноа и сов равны, то HA равно св. Значит трапеция равнобедренная и углы при основании трапеции равны. У Нав и Сав у них сторона ав общая. Получается у этих треугольников равны по две стороны и угол между ними. Есть такой признак. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого, то такие треугольники равны

Ну АВ общая сторона, сторона HA=CB по условию, так как треугольники равны. Соответственно HO=CO, AO=OB, значит HO+OB=CO+OA. Равенство третьей стороны доказано. Не так разве?

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Я бы от этого исходила. СВ =НА, потом вторая из суммы равных треугольников . И угол тоже исходя из равенства треугольников изначально данных.
Это первые мысли , может там если более быстрый путь😀
Надо почитать теоремы, которые проходит.

А я не понимаю в чем сложность.
САВ и НАВ каждый состоят из двух треугольников. Один из которых общий, а вторые части равны

И никаких данных больше? 😳 Послушаю ответы, кажется 🤦

Я щас может тупану, но линейкой измерить 😅😅😅😅